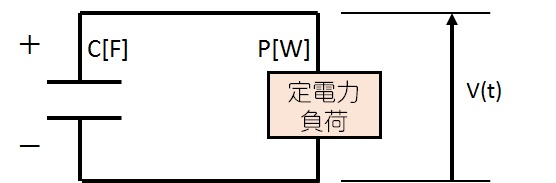
充電されたコンデンサに、 DC/DCコンバータなどの「定電力負荷」を接続した場合の挙動について考えます。

コンデンサの容量を\( C \mathrm{[F]} \)、初期電圧を\( V(0)=V_0\)、 とし、定電力負荷\( P\mathrm{[W]} \)を接続した場合を考えます。 このとき、
に着目すると、次式が成立します。
また、ある電圧 \( V(t)\)となるまでの秒数は、式(1)を\( t \)について解き、
となります。
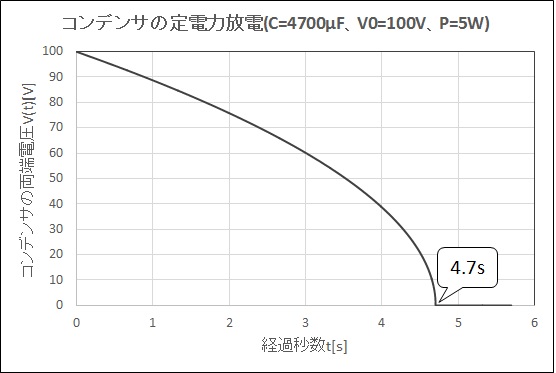
上式(1)に従い、\( C=4700\mu \mathrm{F} \)、\( V_0=100\mathrm{V} \)、\( P=5\mathrm{W} \)、とした場合の\( V(t) ― t \)グラフは次の通りとなります。 また(2)より、放電開始より\( 4.7\mathrm{sec} \)で放電完了(\( V(t) = 0\mathrm{V} \))と求められます。
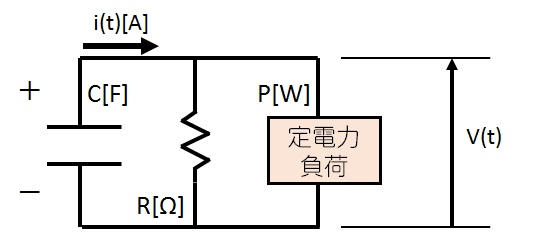
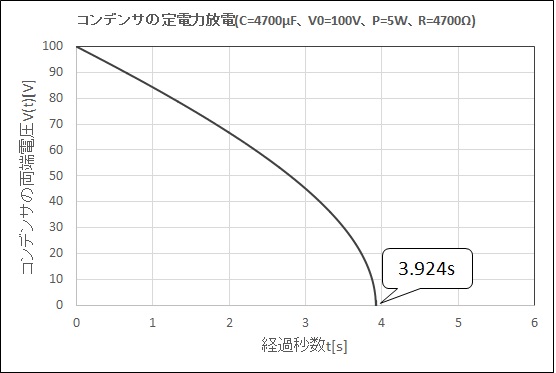
次に、定電力負荷に加え、\( \mathrm{R[\Omega]} \)の抵抗器を並列に接続した場合を考えます。 コンデンサより図の方向に流れ出す電流を\( i(t) \mathrm{[A]} \)とおくと、電荷\( Q(t) \)の定義より
\[ Q(t)=\int^t_0 i(t) dt \tag{3} \]従って、微小時間\( \Delta t \)経過後のコンデンサの電荷が\( Q(0) \to Q(0) - \Delta Q \)になるとすれば、
\[ \Delta Q = i(0) \Delta t \tag{4} \]また、電流\( i(t) \)については、抵抗器に流れる電流が\( V(t)/R \)、定電力負荷に流れる電流が\( P/V \)であるため、
\[ i(t) = \frac{V(t)}{R} + \frac{P}{V(t)} \tag{5} \]以上の式(4),(5)より、微小時間\( \Delta t \)経過後のコンデンサの両端電圧は、
\[ \begin{eqnarray*} V(\Delta t) &=& \frac{1}{C} \left( Q(0) - \Delta Q \right)\\ &=& V_0 - \frac{1}{C} \left( \frac{V_0}{R} + \frac{P}{V_0} \right)\Delta t\tag{6} \end{eqnarray*} \]また、さらに微小時間\( \Delta t \)経過後のコンデンサの両端電圧は、 同様の作業を繰り返し、
\[ V(\Delta t + \Delta t) = V(\Delta t)- \frac{1}{C} \left( \frac{V(\Delta t)}{R} + \frac{P}{V(\Delta t)} \right)\Delta t\tag{7} \]以上を繰り返すことで、コンデンサの両端電圧\( V(t) \)について、数値的に求めることができます。 実際に、刻み幅\( \Delta t = 0.001 \)とし、Microsoft Excelで計算した結果を下記に示します。 ただし、\( C=4700\mu \mathrm{F} , V_0=100\mathrm{V} , P=5\mathrm{W} , R=4700\mathrm{\Omega} \)としました。 放電完了まで3.924secであり、Case1と比較し放電用抵抗器の影響が出ていることが分かると思います。